SSCI-581-Week7
Map Projections: From 3D to 2d
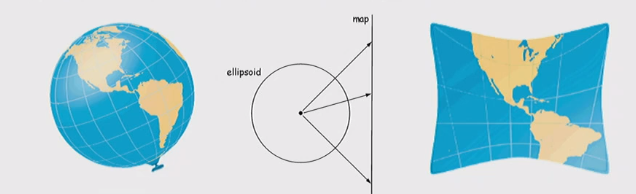
Map Projection = Mathematical Operation
- Map projection is a mathematical operation that transforms the surface of a 3D ellipsoid to a 2D surface
- The mathematical operation used for a particular projection is chosen based on the parameters
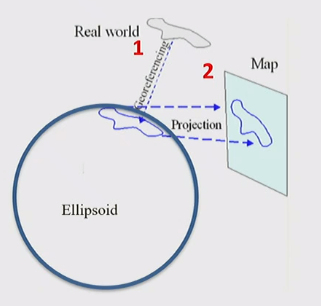
Process (Georeferencing, then Projecting)
- A two-step process transforms the real world to a map projection:
- A chosen coordinate system is used to locate real-world features onto the ellipsoid
- The surface of the ellipsoid is then mathematically transformed to a 2D surface
Four Characteristics of the Globe
-
Shapes
- Shape is the outline of a polygon
-
Area
- Area is the size of a polygon and its value relative to other polygon
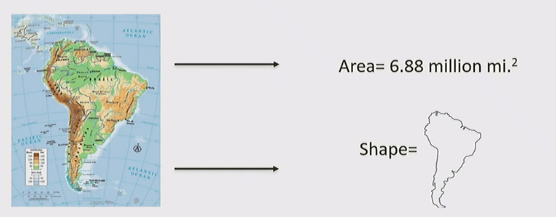
- Area is the size of a polygon and its value relative to other polygon
-
Distance
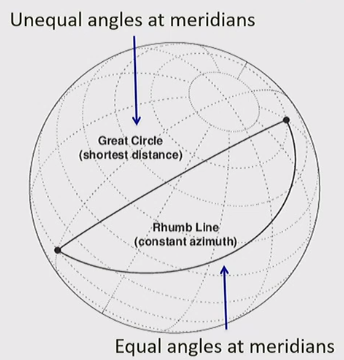
- The shortest distance between any two points on the globe sits on a circumference of the globe, called a great circle path
- The equator, all meridians, and any other circumference is a great circle path
- On a map, the shortest distance often looks like a straight line, but depending on the projection and the points, it may be drawn as a curved line
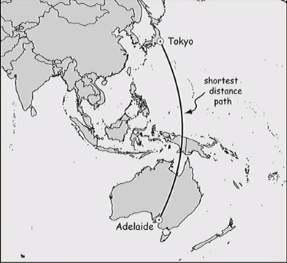
- The shortest distance between any two points on the globe sits on a circumference of the globe, called a great circle path
-
Direction
- Directions (azimuths) are measured as angles from meridians
- A rhumb line is a line crossing all meridians of longitude at the same angle (a line of constant bearing) (eg. the in the below image)
- They are useful when relying on a compass
- Mercator projection is notable since a straight line between two points is a rhumb line
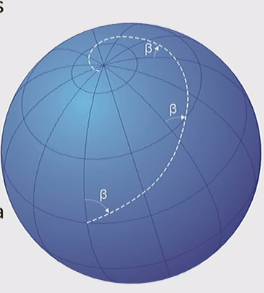
Rhumb lines vs. Great Circles
- A rhumb line / line of equal bearing differs from a great circle
- Rhumb line: lines of equal angles to meridians
- Great circles: lines of shortest distance on circumference, having changing angles as you cross meridians
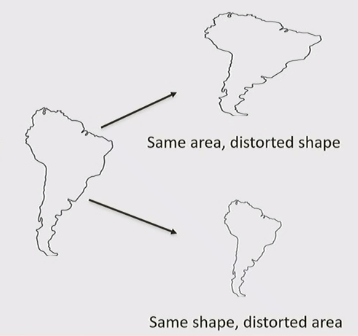
Distortions of Four Globe Characteristics
-
Shape and Areas
- Shape: the shape of the polygons odes not hold true; i.e. a square gets stretched to a rectangle
- Area: the ratio of sizes of polygons on the globe and on the map does not hold true
-
Distance and Direction
- Distance: the ratio of lengths of lines between points on the globe and no the map does not hold true
- Direction: the angles between points on the globe does not hold true
Projection Parameters
- Four Projection Parameters:
- Developable Surace
- Point of Projection
- Point/Line(s) of Contact
- Aspect
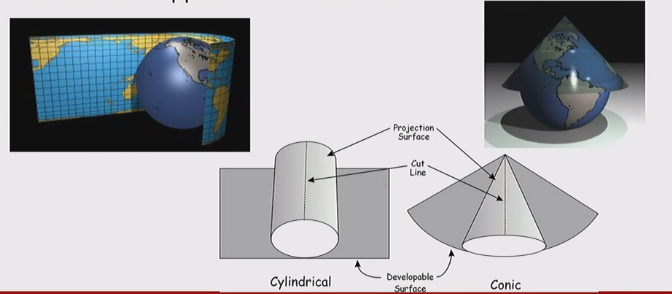
Developable Surface
- The developable surface (also called the projection surface) is the 2D surface that is the result of the mathematical operation of projection
- Three types of developable surface:
- cylinder developable surface
- conic developable surface
- Planar developable surface
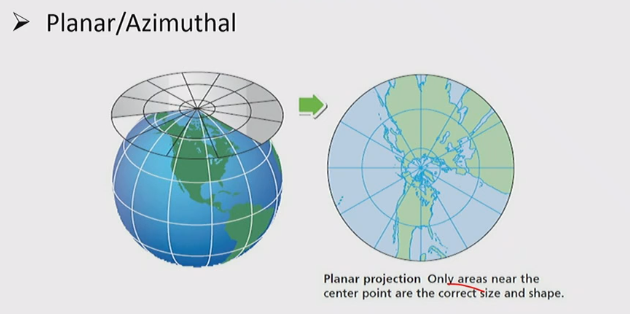
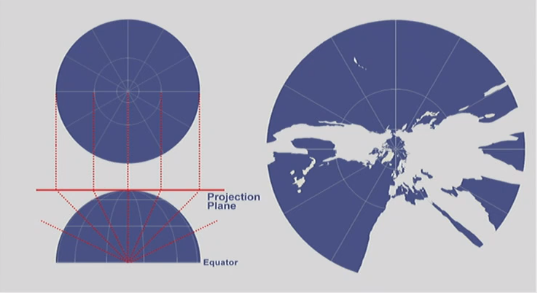
Point of Projection
- The point of projection is the point from which the projection is initiated / the perspective point
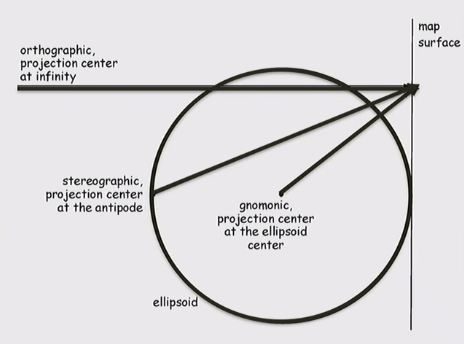
Point of projection is center of ellipsoid
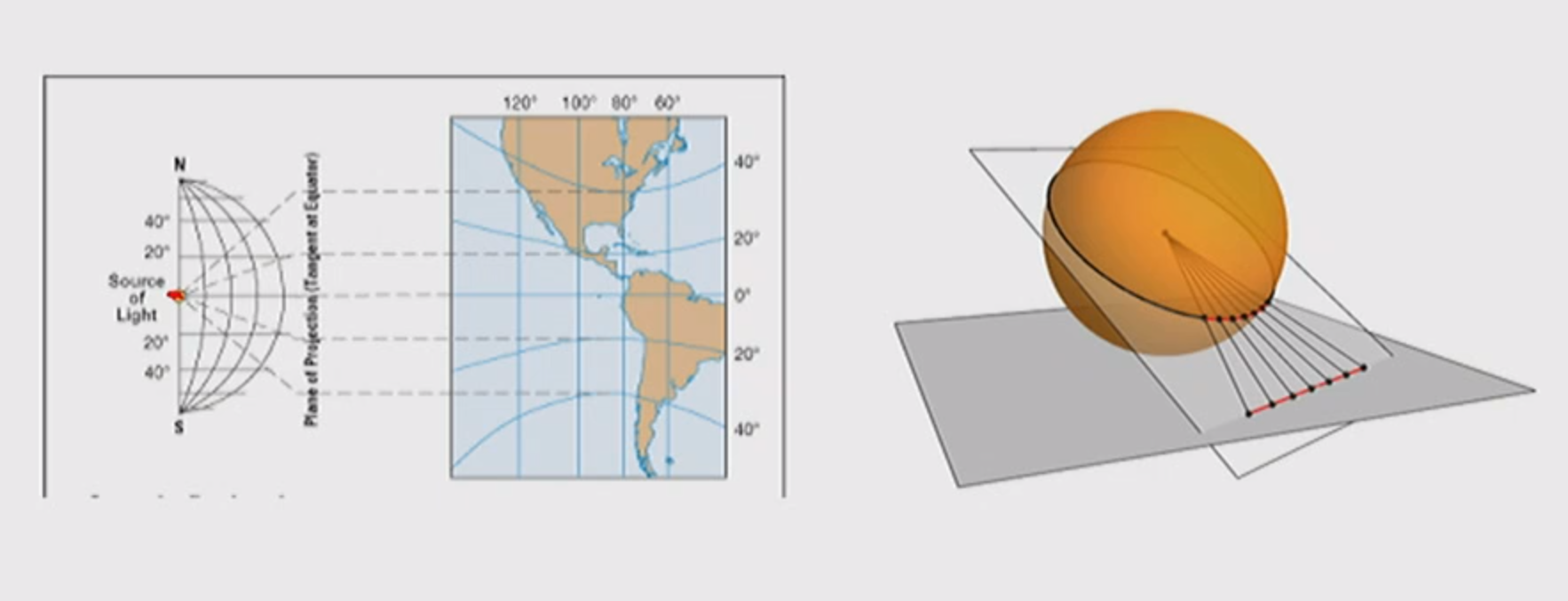
Point of projection is antipode(opposite point on ellipsoid) to point of contact
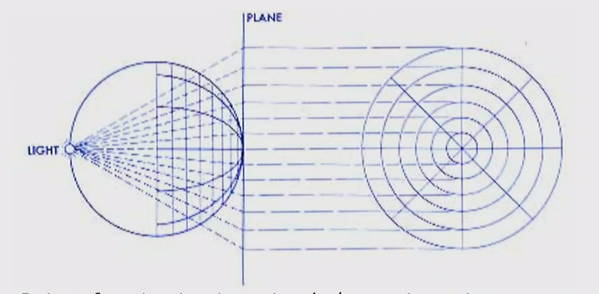
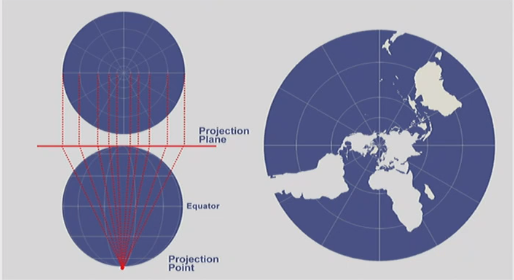
Point of projection is infinity
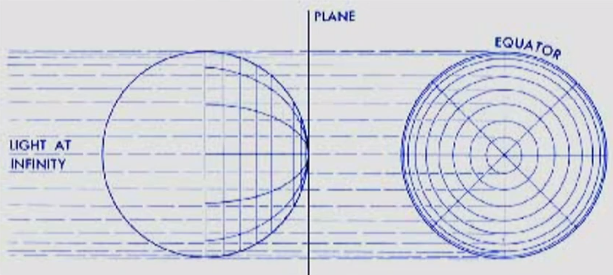
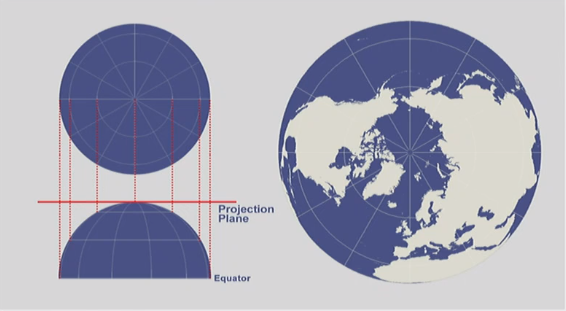
Aspect
- Orientation of the developable surface to the globe
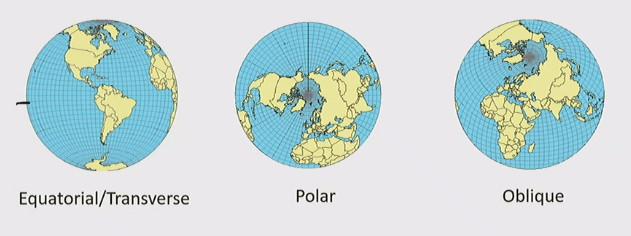
Point/Line(s) of Contact
- two type of contact
- Tangent
- Secant
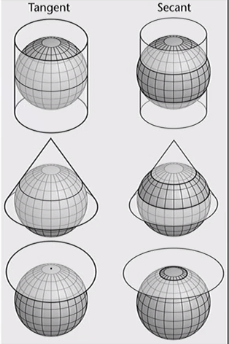
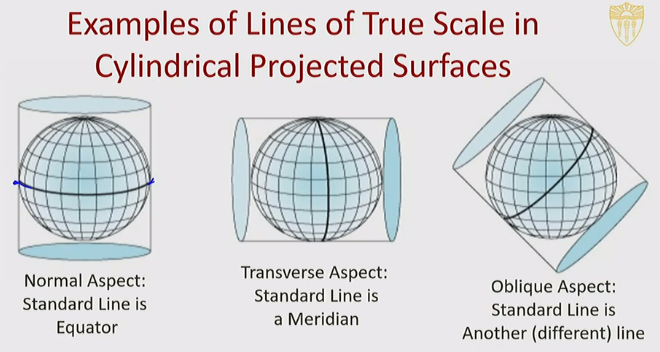
Standard Line: Line of True Scale
- lines of contact are lines of true scale - the ratio of distance between the ellipsoid and line of contact hold true
General Principle for choosing a Map Projection
- Consider what type of accuracy is most important for your purpose
- Remember a map projection is always most accurate - in all respects - near its center
Projected Coordinate System
Benefits of PCS
-
PCS make communication and calculation easier
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Comment


