动态规划 （Dynamic Programming）

动态规划问题的通性

动态规划问题一般都是用来求最值的，例如最长递增子序列，最小编辑距离等等。动态规划的核心思路是穷举， 因为要求最值，肯定要知道所有的值是什么才能知道最值是多少。

怎么穷举以及如果优化穷举便是我们研究的问题。

动态规划的三要素

重叠子问题、最优子结构、状态转移方程是动态规划的三要素。

定义一个状态转移方程，有以下思维框架：
明确base case -> 明确[状态] -> 明确[选择] -> 定义dp数组/函数的含义

动态规划算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
    for 选择 in 所有可能的选择:
        # 此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    return result

# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

例子：凑零钱问题

力扣第322题 [ 零钱兑换 ]

给你k种面值的硬币，面值分别为c1, c2, c3,....ck，每种硬币的数量无限，请你求出凑够amount金额所使用的最小硬币数。如果不可能凑出，请返回-1. 例如，amount = 11, c1 = 1, c2 = 2, c3 = 5。 则最少需要三枚硬币凑出 11 = 5 + 5 + 1

  1. 问题符合最优子结构
    要符合最优子结构，子问题之间必须相互独立。例如，考试中的每门科目都是项目独立的，要考到最高分，就需要每科考到最高分。每科考到最高分，那么该科中的每种题型都要拿到最多的分。 每门科目之间、每个题型拿到最高分之间是相互独立的。反之，如果你的语文成绩和数学成绩相互制约，一个拿最高分，另一个就不能那最高分，那他们之间就不是相互独立的，就破坏了最优子结构的相互独立性。

    该题是符合最优子结构的，因为硬币有无限枚，我们要求凑出11的最少硬币，就需要求得凑出 10，9，6三种金额的最少硬币数，然后加1. 求出凑齐10，9，6的最少硬币数量，就要求他们的子问题最小值然后加1.可以看出子问题之间是相互独立的。

  2. 状态转移方程

    1. base case, 该问题中就是amount数值为0的时候，不需要任何硬币就可以凑出amount
    2. 确定[状态]，也就是原问题和子问题中会变化的量， 由于硬币数量无限，在子问题中amout值会不断趋近于0（base case），所以状态就是amout的值
    3. 确定[选择]， 也就是导致[状态]变化的行为，在该题中，即为不同的硬币面值。
    4. 明确dp函数/数组的定义。 一般来说函数的参数就是状态转移中会变化的量，也就是状态；函数的返回值就是题目要求我们计算的量。这样我们可以定义一个dp函数： dp(n)表示，输入一个目标金额n, 返回凑出目标金额n所需的最少硬币数量。

根据以上我们可以写出伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 伪码框架
int coinChange(int[] coins, int amount) {
    // 题目要求的最终结果是 dp(amount)
    return dp(coins, amount)
}

// 定义：要凑出金额 n，至少要 dp(coins, n) 个硬币
int dp(int[] coins, int n) {
    // 做选择，选择需要硬币最少的那个结果
    for (int coin : coins) {
        res = min(res, 1 + dp(coins, n - coin))
    }
    return res
}

加入base case 完整的代码就可以写出来了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int coinChange(int[] coins, int amount) {
    // 题目要求的最终结果是 dp(amount)
    return dp(coins, amount)
}

// 定义：要凑出金额 n，至少要 dp(coins, n) 个硬币
int dp(int[] coins, int amount) {
    // base case
    if (amount == 0) return 0;
    if (amount < 0) return -1;

    int res = Integer.MAX_VALUE;
    for (int coin : coins) {
        // 计算子问题的结果
        int subProblem = dp(coins, amount - coin);
        // 子问题无解则跳过
        if (subProblem == -1) continue;
        // 在子问题中选择最优解，然后加一
        res = Math.min(res, subProblem + 1);
    }

    return res == Integer.MAX_VALUE ? -1 : res;
}

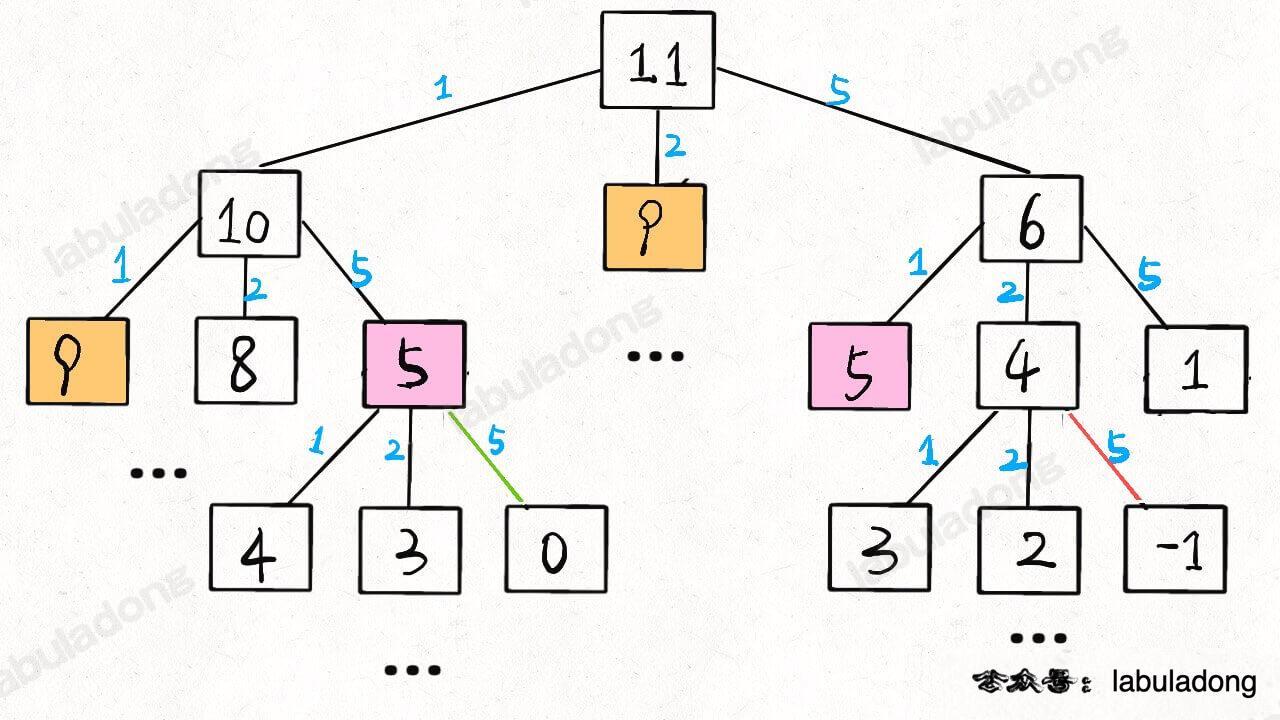
接下来就是去优化整个递归穷举过程，因为这里面存在重叠子问题，一些金额所需要的硬币数量我们已经算过，如下图，金额为9、5的在不同分支中出现了多次，可以把它们存在备忘录中，如果在另一个树分支中用到了，直接调用即可，不用重复计算，即[剪枝]。

带备忘录的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    int[] memo;

    int coinChange(int[] coins, int amount) {
        memo = new int[amount + 1];
        // 备忘录初始化为一个不会被取到的特殊值，代表还未被计算
        Arrays.fill(memo, -666);

        return dp(coins, amount);
    }

    int dp(int[] coins, int amount) {
        if (amount == 0) return 0;
        if (amount < 0) return -1;
        // 查备忘录，防止重复计算
        if (memo[amount] != -666)
            return memo[amount];

        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            // 计算子问题的结果
            int subProblem = dp(coins, amount - coin);
            // 子问题无解则跳过
            if (subProblem == -1) continue;
            // 在子问题中选择最优解，然后加一
            res = Math.min(res, subProblem + 1);
        }
        // 把计算结果存入备忘录
        memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
        return memo[amount];
    }
}