回溯法

回溯法的本质

回溯法本质上是一种暴力穷举算法，它可DFS相似，都是通过遍历所有可能的情况，选出符合条件的选择组成的路径。回溯法和DFS细微的差别是回溯算法是在遍历树枝，DFS算法实在遍历节点

回溯法的框架

站在回溯树的一个节点上，要考虑三个问题：

  • 路径：也就是已经做出的选择
  • 选择列表：也就是你当前可以做的选择
  • 结束条件：也就是到达决策树底层，无法再做选择的条件

代码框架：

1
2
3
4
5
6
7
8
9
10
11
result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是for循环里面的递归，再递归调用之前做选择，在递归调用之后撤销选择

例子：力扣第46题全排列

全排列问题，我们一般的思路是先固定第一位，然后穷举第二位，再第二位穷的时候，也是固定第二位，穷举第三位，以此类推，其实就形成了一棵回溯树。以长度为3的[1,2,3]数组作为例子，我们可以得到如下的回溯树：

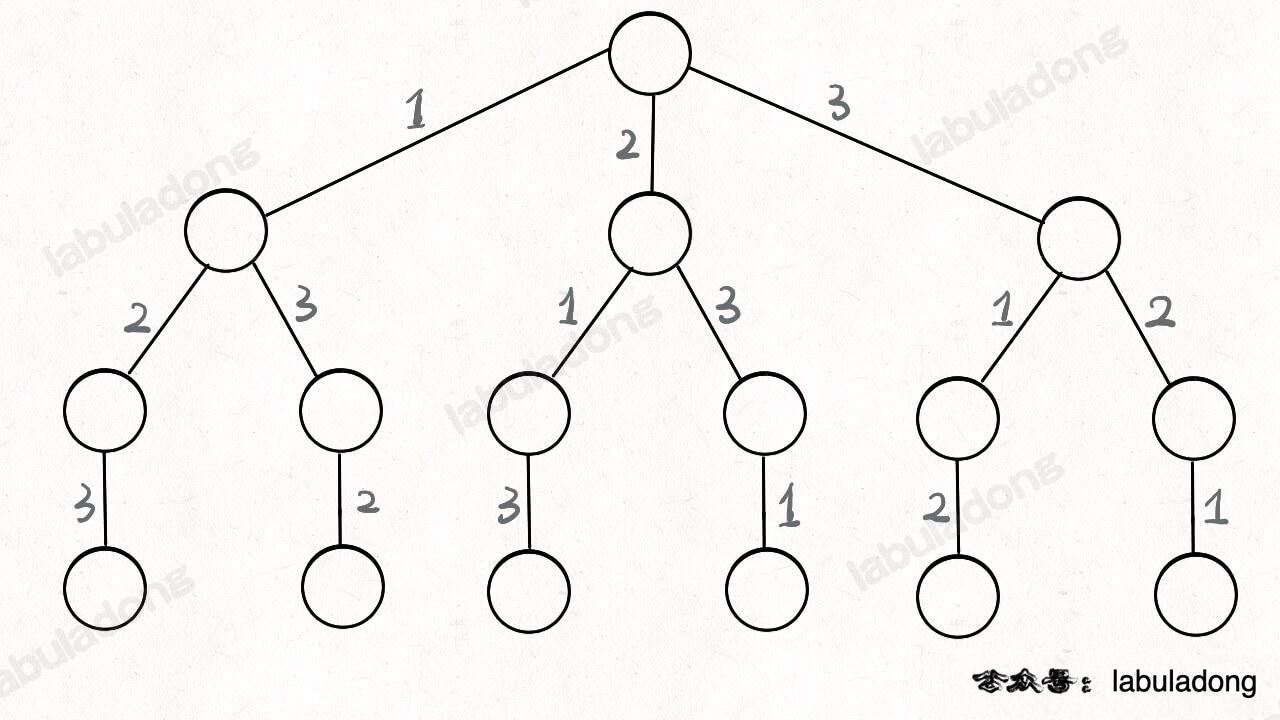
只要遍历这棵树，记录路径上的数字，就是所有的全排列。站在其中一个节点上，我们就需要考虑当前可以做的选择有哪些。例如：

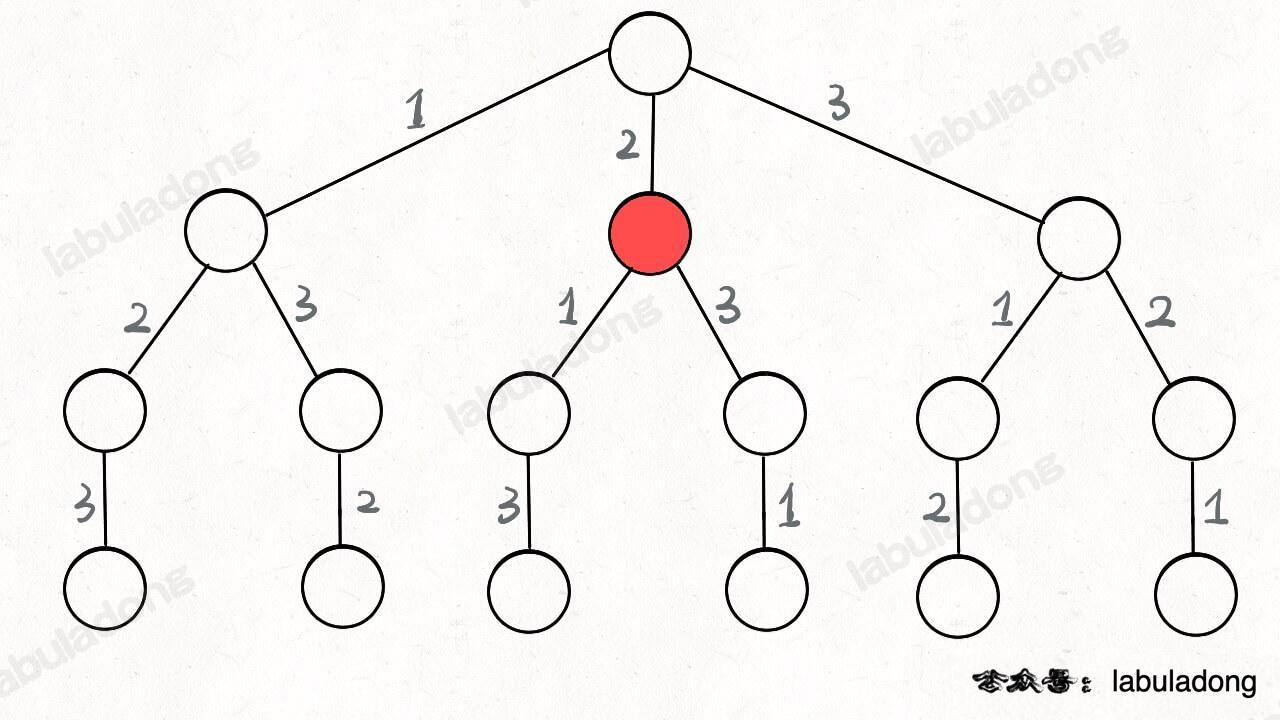
再2这个节点上，我们可以选择1或者3，其中[2]就是我们走过的路径，记录着我们已经做的选择，[1,3]就是选择列表，表示我们当前可以做的选择。结束条件就是我们到达叶子节点，也就是选择列表为空的时候。

我们定义的backtrack函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性。

那如何遍历一棵树呢？
其实就是遍历一棵多叉树的框架：

1
2
3
4
5
6
7
8
void traverse(TreeNode root) {
    for (TreeNode child : root.childern) {
        // 前序位置需要的操作
        traverse(child);
        // 后序位置需要的操作
    }
}

回溯法解决排列/组合/子集问题